FP-Growth挖掘频繁项，java实现

FP-Growth主要是用来进行挖掘频繁项，使用场景是发现事物之间的相关性，其中用支持度表示相关性的大小，可以通过设置支持度来筛选相关性小的事物的联系。相比较于Apriori算法需要扫描多次数据，严重受到IO的影响。FP-Growth只需要扫描两次数据集，可以提高算法运行效率。下图是论文中的图：

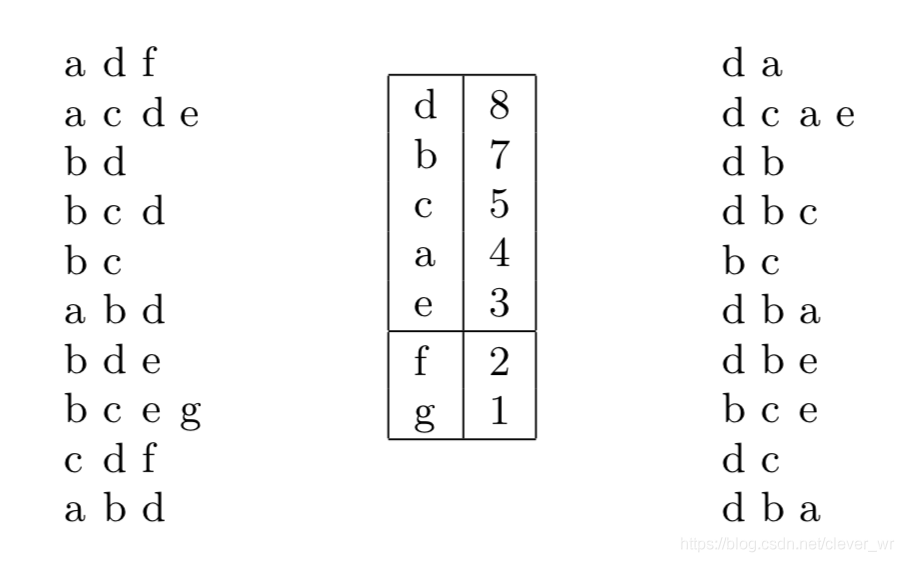
左边表示初始的数据集，表示原始的相关关系。然后遍历左边数据集，统计每个元素的出现次数，然后按照出现次数降序排列。得到中间的表格，设置minSupport = 3，然后删除出现次数小于minSupport的所有元素，然后遍历重构左侧原始元素之间的关系（删除出现次数小于minSupport的所有元素,同时以行为单位按照总出现次数降序重新排列）得到右边数据集（比如左第一行中f出现次数是2 < 3，因此删除f得到新关系[d,a]）。（遍历两次，因此扫描了两次数据）。

设置minSupport：

    private int minStep = 1;     public int getMinStep() {         return minStep;     }      public void setMinStep(int minStep) {         this.minStep = minStep;     }

然后就是构建一棵FP树，因此需要构建一个节点的结构体，由于使用java实现因此创建了一个FPTreeNode类：

    private class FPTreeNode {         int count = 0; //访问次数         int blockAddress = 0;//指的是元素，由于我主要是用来统计blockAddress之间的关系，因此这样取名字         FPTreeNode parent = null;//记录父节点         FPTreeNode nextSimilarNode = null; //记录指向下一个该元素的节点         List<FPTreeNode> childSet = new ArrayList<>();         public FPTreeNode(int blockAddress) {             this.blockAddress = blockAddress;             count = 1;         }     }

构成的图如下图所示（蓝色线指的是：nextSimilarNode，红色线指的是：parent）

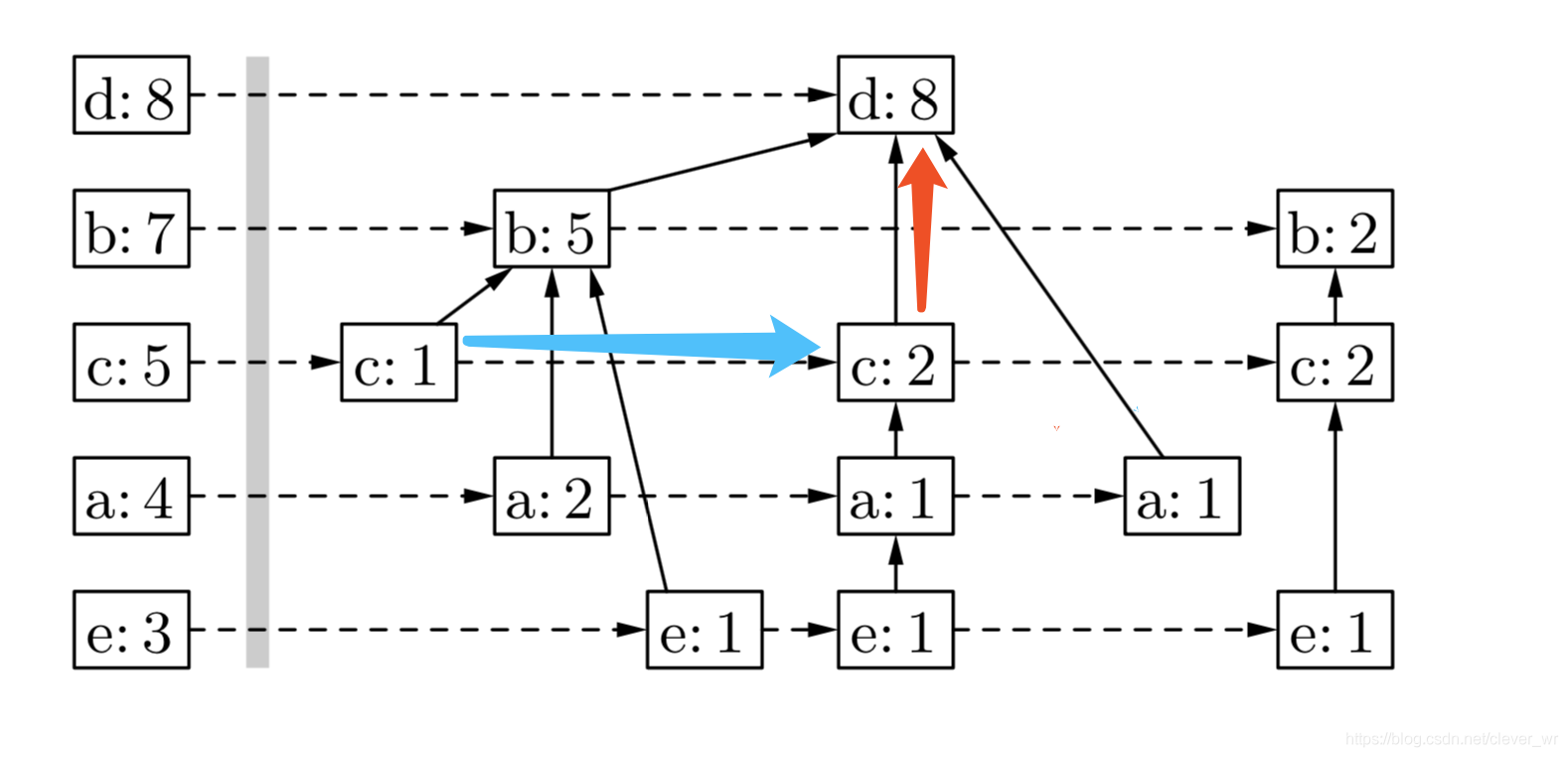
构建上图FP树主要分三步：

1.首先需要遍历数据集，统计元素出现总次数

    //计算各基本blockAddress出现的频次。     public List<List<Integer>> init(File file) {         List<List<Integer>> lists = new ArrayList<>();         try {             BufferedReader bufferedReader = new BufferedReader(new FileReader(file));             String string = "";             double start = -1.0;              List<Integer> list = new ArrayList<>();             List<Integer> listCount = new ArrayList<>();             double timePeroid = 60.0;             while((string = bufferedReader.readLine()) != null) {                 //time peroid, start block, access count                 String[] s = string.split(",");                 if (start == -1.0) {                     start = Double.valueOf(s[0]) + timePeroid;                 }                 if (start > Double.valueOf(s[0])) {                     if (!list.contains(Integer.valueOf(s[1]))) {                         list.add(Integer.valueOf(s[1]));                         listCount.add(Integer.valueOf(s[2]));                     }                 } else {                     lists.add(new ArrayList<>(list));                     listsCount.add(new ArrayList<>(listCount));                     start = Double.valueOf(s[0]) + timePeroid;                     list.clear();                     listCount.clear();                     list.add(Integer.valueOf(s[1]));                     listCount.add(Integer.valueOf(s[2]));                 }             }             if (list.size() > 0) {                 lists.add(new ArrayList<>(list));                 listsCount.add(new ArrayList<>(listCount));             }             bufferedReader.close();         } catch (FileNotFoundException e) {             e.printStackTrace();         } catch (IOException e) {             e.printStackTrace();         }         return lists;     }

2. 根据minSupport进行筛选生成项头表，同时按出现频次降序排列。

public List<FPTreeNode> buildTable(List<List<Integer>> lists) {         List<FPTreeNode> trees = new ArrayList<FPTreeNode>(); //获得频繁项表头，删除了小于minSupport的。         if (lists.size() == 0) {             return null;         }         HashMap<Integer, FPTreeNode> hashMap = new HashMap<>();         for (int i = 0; i < lists.size(); i++) {             List<Integer> tmp = lists.get(i);             for (int j = 0; j < tmp.size(); j++) {                 int val = tmp.get(j);                 if (hashMap.containsKey(val)) {                     hashMap.get(val).count++;                 } else {                     hashMap.put(val, new FPTreeNode(val));                 }              }         }         Iterator<Map.Entry<Integer, FPTreeNode>> iterator = hashMap.entrySet().iterator();         while(iterator.hasNext()) {             Map.Entry<Integer, FPTreeNode> entry = iterator.next();             if (entry.getValue().count >= minStep) {                 trees.add(entry.getValue());             }         }         //将频繁项进行降序排列         Collections.sort(trees, new Comparator<FPTreeNode>() {             @Override             public int compare(FPTreeNode o1, FPTreeNode o2) {                 if (o1.count < o2.count) {                     return 1;                 } else {                     if (o1.count > o2.count) {                         return -1;                     }                 }                 return 0;             }         });         return trees;     }

3.通过递归，构建FP树。自底向上。具体流程如下图：（红色箭头表示处理流程，蓝色“阴影” FP树为创建的投影。）

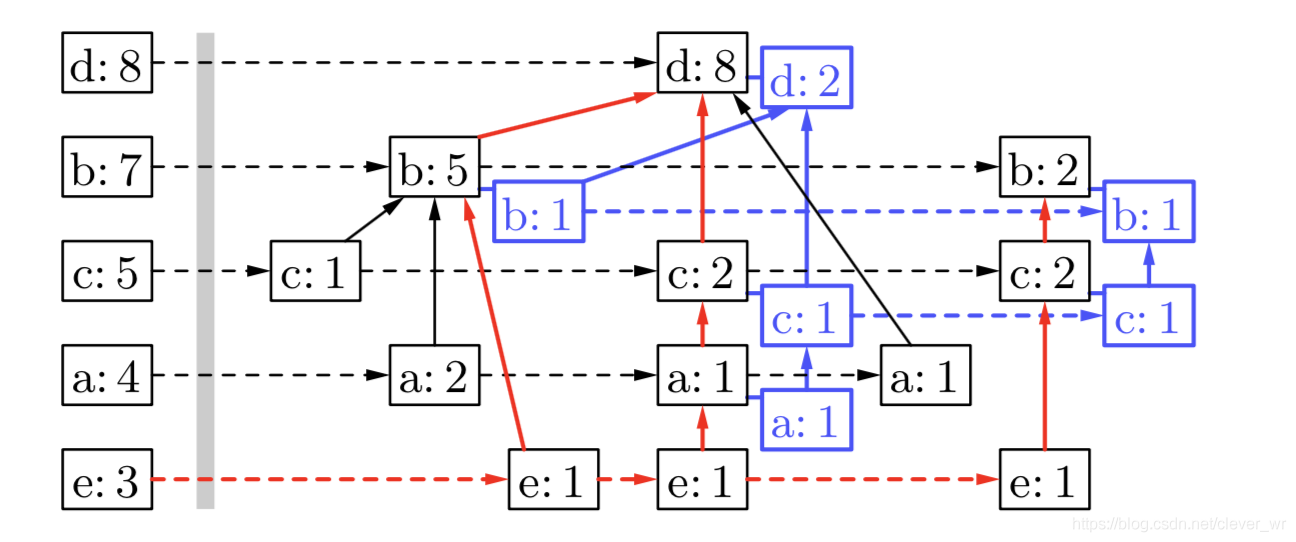
/**      * 返回一个降序且满足频繁项的list      * @param list      * @return      */     public List<Integer> sortbyTrees(List<Integer> list, List<FPTreeNode> trees) {         List<Integer> tmp = new ArrayList<>();//返回一个降序且满足频繁项的list         for (int i = 0; i < trees.size(); i++) {             int block = trees.get(i).blockAddress;             if (list.contains(block)) {                 tmp.add(block);             }         }         return tmp;     }     public FPTreeNode findChild(FPTreeNode root, int node) {         for (FPTreeNode treeNode : root.childSet) {             if (treeNode.blockAddress == node) {                 return treeNode;             }         }         return null;     }     public void addNode(FPTreeNode node, List<Integer> list, List<FPTreeNode> trees) {         if (list.size() > 0) {             int val = list.remove(0);             FPTreeNode node1 = new FPTreeNode(val);             node1.parent = node;             node.childSet.add(node1);             for (FPTreeNode treeNode : trees) {                 if (treeNode.blockAddress == val) {                     while (treeNode.nextSimilarNode != null) {                         treeNode = treeNode.nextSimilarNode;                     }                     treeNode.nextSimilarNode = node1;                     break;                 }             }             addNode(node1, list, trees);         }     }     public FPTreeNode buildFPTree(List<List<Integer>> lists, List<FPTreeNode> trees) {         FPTreeNode root = new FPTreeNode(0);         for (int i = 0; i < lists.size(); i++) {             List<Integer> tmp = sortbyTrees(lists.get(i), trees);//得到一个降序且满足频繁项的list             FPTreeNode subRoot = root;             FPTreeNode tmpRoot = root;             if (root.childSet.size() > 0) {                 while (tmp.size() > 0 && (tmpRoot = findChild(subRoot, tmp.get(0))) != null) {                     tmpRoot.count++;                     subRoot = tmpRoot;                     tmp.remove(0);                 }             }             addNode(subRoot, tmp, trees);         }         return root;     }

4.按照FP-Growth算法挖掘频繁项，从底向上。

 public void FPGrowth(List<List<Integer>> transRecords, List<Integer> postPattern) {         List<FPTreeNode> trees = buildTable(transRecords);// 构建项头表，同时也是频繁1项集         // 构建FP-Tree         FPTreeNode root1 = buildFPTree(transRecords, trees);         if (root1.childSet.size() == 0) {             return;         }         if (postPattern.size() > 0) {             for (FPTreeNode node : trees) {                 System.out.print(node.count + ":" + node.blockAddress);                 for (int val: postPattern) {                     System.out.print(" " + val);                 }                 System.out.println();             }         }         for (int i = trees.size() - 1; i >= 0; i--) {             FPTreeNode node = trees.get(i);             List<Integer> tmp = new ArrayList<>();             tmp.add(node.blockAddress);             if (postPattern.size() > 0) {                 tmp.addAll(postPattern);             }             // 寻找header的条件模式基，放入records中             List<List<Integer>> records = new ArrayList<>();             FPTreeNode nextNode = node.nextSimilarNode;             while (nextNode != null) {                 int cnt = nextNode.count;                 List<Integer> prenodes = new ArrayList<Integer>();                 FPTreeNode parent = nextNode;                 while ((parent = parent.parent) != null && parent.blockAddress != 0) {                     prenodes.add(parent.blockAddress);                 }                 while (cnt > 0) {                     cnt--;                     records.add(prenodes);                 }                 nextNode = nextNode.nextSimilarNode;             }             FPGrowth(records, tmp);         }     }

亲测是正确的，数据集格式是：（主要是为了判断第二列之间的相关性，按照第一列表示秒，每180s所包含第二列元素表示为一个关系序列）

60,2104409088,1486 120,2104409088,667 120,2104410112,783 180,2104410112,1467 240,2104410112,1152 240,2104411136,301 300,2104411136,1447 360,2104411136,1429 420,2104411136,225 420,2104412160,1209 480,2104412160,1470 540,2104412160,722 540,2104413184,715 600,2104413184,1455

生成关系序列为：

[[2104409088, 2104410112], [2104410112, 2104411136], [2104411136, 2104412160, 2104413184], [2104413184]]

最后得到的频繁项为：（由于数据量小，频繁项表现不明显）

1:2104413184 2104412160 1:2104411136 2104412160 1:2104413184 2104411136 2104412160 1:2104410112 2104409088 1:2104411136 2104413184 1:2104410112 2104411136